コンピューターは2進法! 宇宙人なら6進法?
「人間の指が十本だから!」
そうなのです。十進法で数を数えるのは、たまたま人間の指が十本であるという理由だけで、数学的には必然性がないのです。
コンピューターは、半導体スイッチのオンとオフ(0と1)で成り立っているので、2進法で計算しています。もし、6本指の宇宙人がいたら、6進法で数を数えるはずです。
ここまで来て、ようやく n進法の意味や意義が理解されます。
理解したことを感覚レベルにまで高めるPUCFlash
ここで終わったら、なんとなく分かったというレベルにとどまります。スッキリと「分かった!」となるために、PUCFlashの数学脳トレーニングの出番です。
PUCFlashトレーニング → n進法になじもう!!
https://bpucservice.com/PUCFlash?DrillID=1634006383579123
十進法で \(1\) から \(10\) までの数を n進法で表す
例えば、\(3\) 進法で表せば、
\(1_{(3)},~\)\(2_{(3)},~\)\(10_{(3)},~\)\(11_{(3)},~\)\(12_{(3)},~\)\(20_{(3)},~\)\(21_{(3)},~\)\(22_{(3)},~\)\(100_{(3)},~\)\(101_{(3)}\)
となります。班の中で教え合いをしながら進めると、「ええ?あれ?あぁ、そうか!」というつぶやきが聞こえます。私はこの時間が好きです!
足し算と引き算
次は足し算と引き算です。筆算でやります。足し算では繰り上がりが生じますが、10進法の筆算の経験はありますから、上の数え上げがしっかりできれば、ほとんどの生徒はできます。
引き算は、繰り下がりが生じます。これは、少し難しいようですが、数え棒のイメージが定着していたら、大丈夫です。
筆算で、\(2341_{(5)}-1432_{(5)}\) を計算してみましょう。
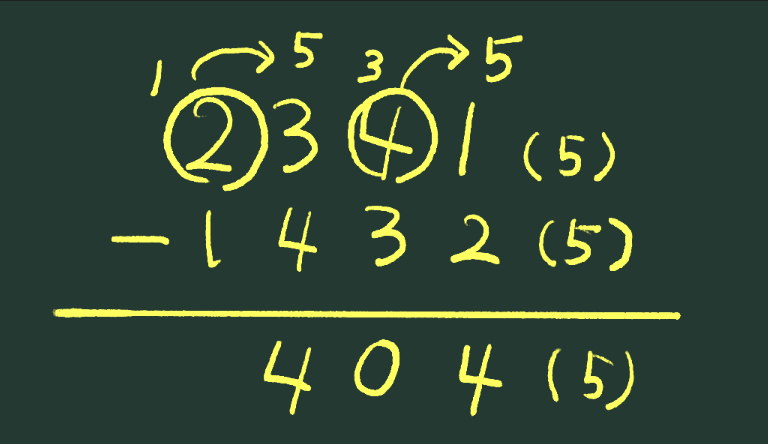
1の位の1から2は引けませんから、上の位の4から1借りてきます。5進法ですから、輪ゴムでとめた5本の数え棒をばらして1と合わせると6になるので、無事に\(2\)引くことができます。
かけ算と割り算
かけ算は、足し算ができたらそれほど難しくありません。
問題は割り算です。どんな数を立てるかは、直感で試行錯誤するのですが、10進法の普通の計算とかなり違う結果になるので、戸惑います。
\(10032_{(3)}\div231_{(4)}\) を筆算で計算してみます。まず、下の○の所にどんな数字を立てることができるか考えます。十進法の感覚では\(3\)かな?と思うのですが、やってみると
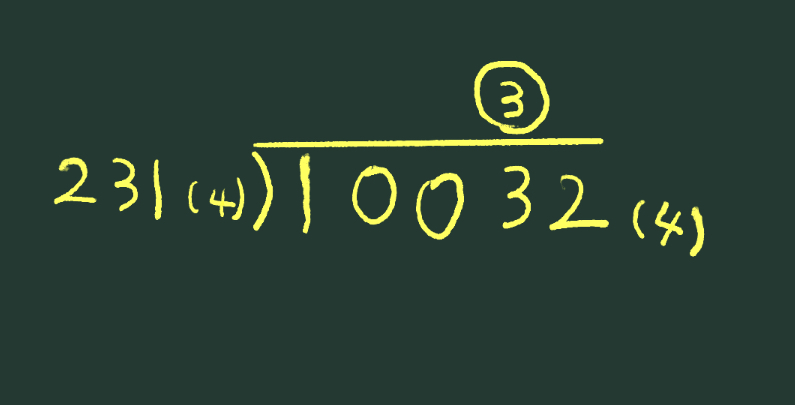
下の計算のように、大幅にオーバーします。次に \(2\)をやってみると、驚いたことに、\(2\)でもオーバーします。
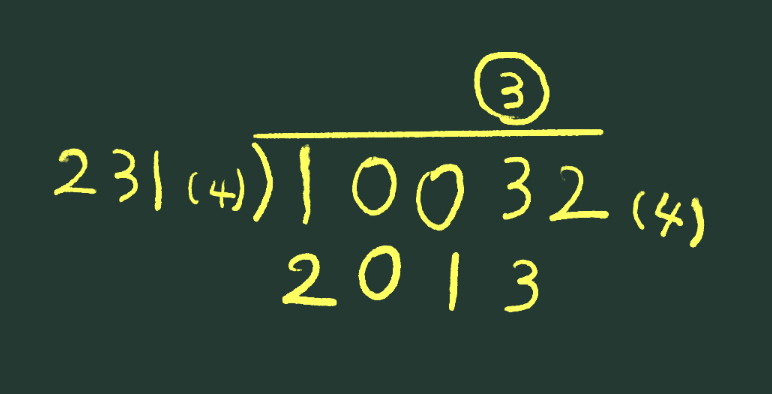
結局、\(1\)しか立てることができず、最後まで計算すると、下のようになります。
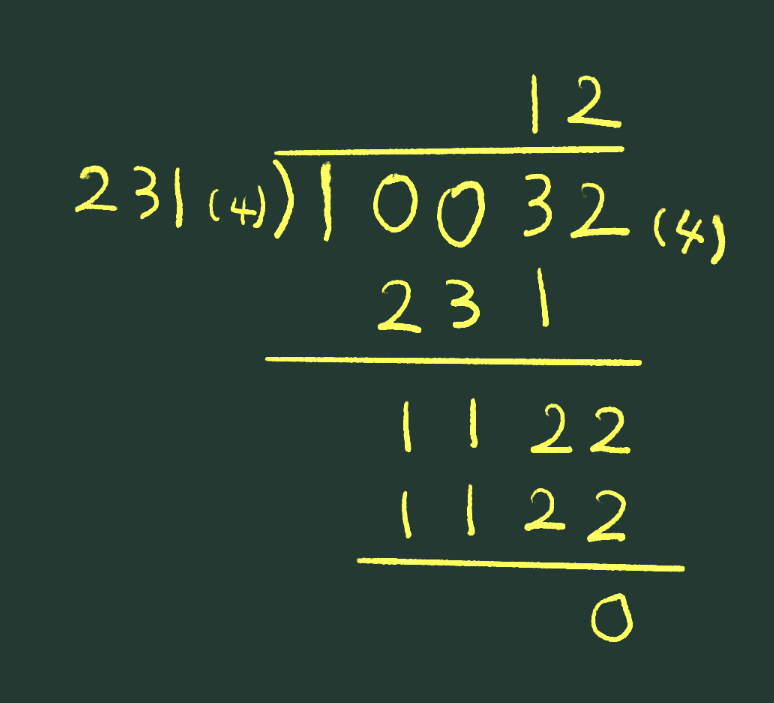
やっと「n進法が分かった!」と納得!
このPUCFlashドリルは、パズルのように面白いみたいで、授業で終わらなかった人は、休み時間になっても、友だちとワイワイ言いながらやっていました。
ここまでやって、生徒は「分かった!」という感想でした。


コメント