このコンテンツは、数学Ⅱの内容です。
ラジアンとは何かが理解できていない人は、「そもそも、「ラジアン」って何ですか?」をお読みください。ここでは、ラジアンが理解できているという前提で、角度がラジアンで与えられたときの三角関数の値を一瞬で求める方法を解説します。
\(\theta\) (ラジアン)が一瞬でイメージできるようにする
三角関数の値を求める方法は、「三角関数の値を一瞬で求める脳トレ」と同じです。°と違って、ラジアンにはなじみがないので、すぐに角度を思い浮かべることができないだけです。
もちろん \(180°=\pi\)(ラジアン)の関係式から、ラジアンを°に直すことはできますが、そんな計算をしていたら、時間がかかります。角度がラジアンで与えられたとき、ラジアンのままでその角度をイメージできるようにトレーニングします。
基準になる\(4\)つの角
まず、基本になるのが、つぎの4つの角度です。\(180\)°\(=\pi\)(ラジアン)ですから、これらは簡単にイメージできますよね。
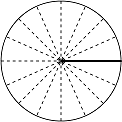
\(\theta=0,~2\pi\)
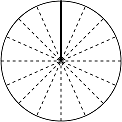
\[\theta=\frac{\pi}{2}\]
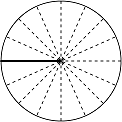
\[\theta=\pi\]
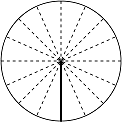
\[\theta=\frac32\pi\]
次は、下の\(3\) つの角度です。これも、\(180\)°\(=\pi\)(ラジアン)の \(\displaystyle\frac16,~\frac14,~\frac13\) ですから、簡単にイメージできると思います。
補助的な \(3\)つの角
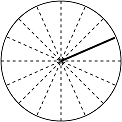
\[\theta=\frac{\pi}{6}\]
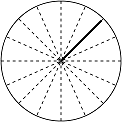
\[\theta=\frac{\pi}{4}\]
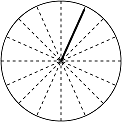
\[\theta=\frac{\pi}{3}\]
基準の角に補助的な角を足したり引いたりして、角度を一瞬でイメージする
例えば、
- \(\displaystyle\frac56\pi\) が出てきたら、\(\pi\) の \(\displaystyle\frac{\pi}{6}\) 手前、と考えます。
- \(\displaystyle\frac54\pi\) の場合は、\(\pi\) の \(\displaystyle\frac{\pi}{4}\) 後ろ、と考えます。
あとは、例によって「視考力」トレーニングを積むことで、一瞬で角度を思い浮かべることができるようになるまで、反復練習します。
下のトレーニングを、まず出題順で「系統的」にイメージを作って、慣れたら、「ランダム」で「視考力」を養います。
PUCFlash トレーニング → 図からラジアン
https://bpucservice.com/PUCFlash?DrillID=1623460623621755
あとは、ひたすら「視考力トレーニング」
角度が与えられたら、一瞬でその動径をイメージできるようになったら、あとは、「三角関数の値を一瞬で求める脳トレ」と同じ方法で、三角関数の値を頭の中で求めます。
PUCFlash トレーニング → 三角関数の値(ラジアン)
https://bpucservice.com/PUCFlash?DrillID=1589724176888124



コメント