そもそも、「ラジアン」って何ですか？

なぜ、ぐるっと１周が360°なのか？

私は、ラジアンの授業の冒頭、「なぜぐるっと１周が360°なのか」というテーマで、生徒にグループ討議をさせます。当たり前すぎて、なぜ、1周が360°なのか、生徒は考えたこともないようです。チコちゃんに「ボーと生きてんじゃないよ！」と叱られそうですね。「当たり前を問い直す」ことは、学びの出発点です。結構、盛り上がります。

1分は60秒、60分で1時間、24時間で1日、365日で1年。この中で、きちんとした根拠があるのは、365日で1年だけです。これは、地球が太陽の周りを1周（公転）する間に、地球が自転する回数で、物理的に決まっています。それ以外は、すべて人間が勝手に決めたものです。

12, 24, 60, 360といった数字が、時間や角度などで使われるのは、約数が多くて、分割しやすいからだと考えられています。例えば、鉛筆を１箱買ってきて、それを兄弟で分ける場面を考えて下さい。1箱10本入りなら、2人と5人の場合しか平等に分けることができません。1箱12本入りなら、2人、3人、4人、6人で、平等に分けることができます。分けるのに便利だから、１ダース＝12個なのです。

1周が360°と決められたのは、①１年が365日で360に近い　②360は約数が多くて、分割がしやすい　という２つの理由からだと考えられます。

数学的に意味のある角度の決め方は？

そもそも、数学では、矛盾がない限り、自由に物事を定義することができます。

例えば、ぐるっと１周は100°と決めても、数学的には何も問題はありません。それが定着しなかったのは、使いにくかったからだけです。例えば、正三角形の角の大きさは、1周が360°なら60°とキレイな数字になりますが、1週が100°なら16.666……°という、とても使いにくい数字になります。

このように角度は分割しやすい方が扱いやすいので、360°が定着したと考えられます。つまり、数学的には必然性がありません。そのことを理解して初めて、ラジアンの意義が理解できます。

なぜ新しい角の単位「ラジアン」を導入するのか？

小学校以来すっかりなじんでいる°という単位があるのに、数学Ⅱでなぜ、「ラジアン」という新しい角度の単位を導入するのでしょうか？

それは、°という角の単位は、日常生活や単純な幾何学では分割しやすく使いやすいのですが、数学で本格的に角を扱おうとすると、とても面倒なことになるからです。「シンプルであることは美しい」というのが数学的な感覚であり、シンプルな定義の方が、シンプルな結果につながるのです。

では、数学的にシンプルな角度の単位の定義は何でしょうか。

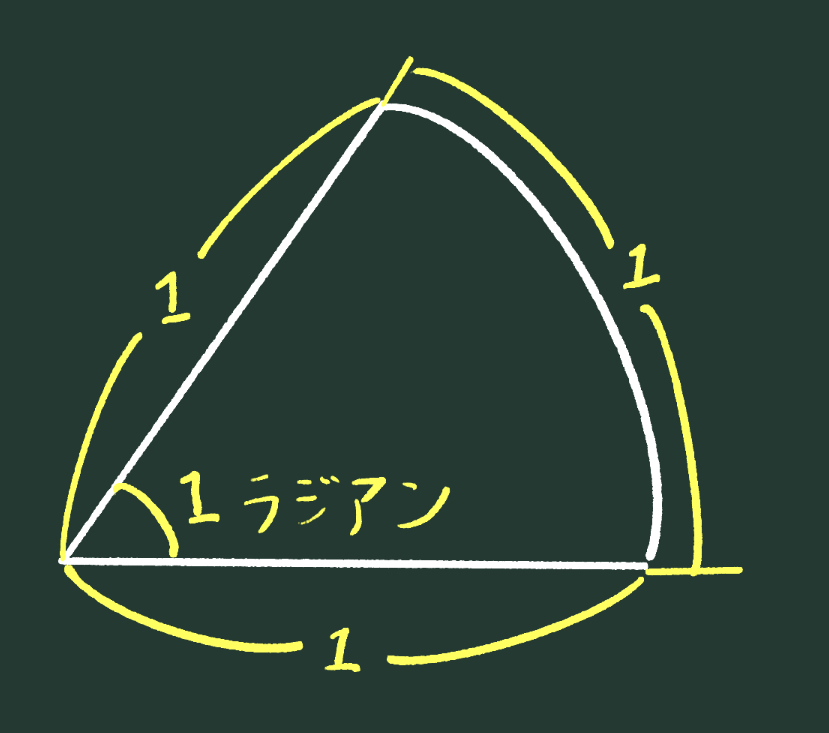
上のように、半径1の扇形の円弧の長さが1のとき、中心角を1と定義すれば、とてもシンプルですね。このように定義した角度の単位を「ラジアン」と言います。英語のradius（半径）に由来します。

最初のうちは、°の方がシンプルで、ラジアンは難しいと感じますが、°は地球の公転周期や約数の数など、色々な要素が混じっていて、実はとても複雑な単位なのです。

扇形の半径を $r$、円弧の長さを $l$、中心角を $\theta$ とすると、単純な比例の関係で、$ l=r\theta$になりますよね。$\theta=\displaystyle\frac{l}{r}$なので、$r$や$l$ に cm などの単位があっても、$\theta$ の単位は、約分されて消えてしまい、単位のない数字「無次元数」になります。ただ、わかりにくい場合は、$1$（ラジアン）などと表記することもあります。

円の中心角は、360°で、半径を1とすると、円周の長さは $2\pi$ です。だから、360° $=\theta$（ラジアン）とすると、$\theta=\displaystyle\frac{l}{r}=\frac{2\pi}{1}=2\pi$ になります。つまり、$360$°$= 2\pi $（ラジアン）となります。そこから、重要な°とラジアンの変換公式、

$$180°=\pi （ラジアン）$$

が出てきます。