三角関数の値を一瞬で求める脳トレ

三角関数の定義

数学Ⅰで三角比の拡張を行う際、教科書のように180°までにとどめるのではなく、数Ⅱを展望して、一気に360°まで拡張することを強くお勧めします。180°までの拡張は、図形としての直角三角形の辺の比を引きずっています。これは、一般角への拡張の理解を、むしろ阻害します。

単位円を用いた三角関数の定義を、直角三角形の辺の比である「三角比」を内包した上位概念として、一気に導入・理解しましょう。

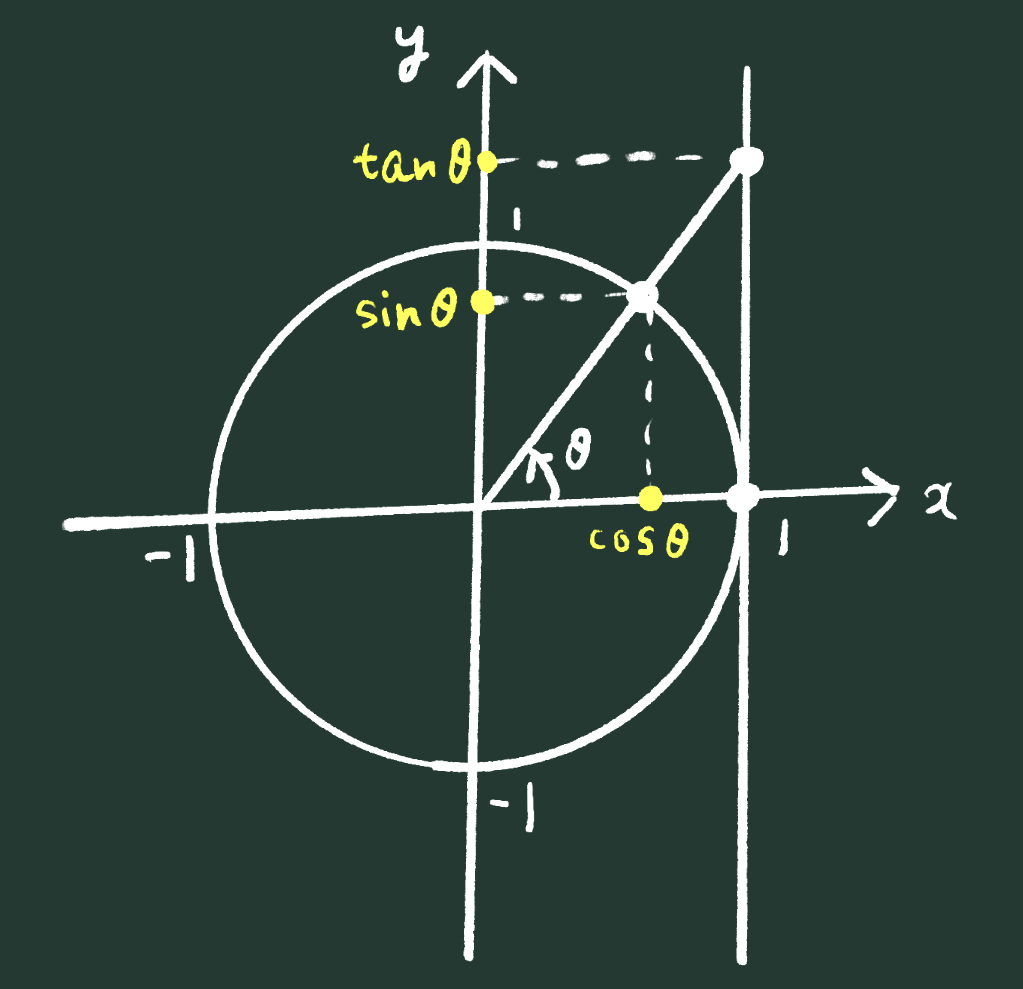
三角関数の一覧表を暗記することは愚の骨頂

生徒の中には、0°～360°までの三角関数の値の一覧表を丸暗記する人がいます。驚くべきことに、そうするように指導する教員もいます。これは愚の骨頂なので、絶対にやめてください！暗記したことは、必ず忘れるし、機械的暗記では三角不等式が解けません。

三角関数の値を一瞬で求める方法（視考力！）

上の定義から、三角関数の値を求めることは、驚くほど簡単です。
私たちの指導を受けた生徒は、ランダムに出題された0°～360°の三角関数の値（51問）を2分以内で求めています！

\(\sin,~\cos\) の場合

\(\pm1,~0\)を除くと、出てくる数字は 3つしかありません。
\(\displaystyle\frac12,~\frac{1}{\sqrt2},~\frac{\sqrt3}{2}\) です。実際はこれに\(\pm\)の符号がつきます。これらを区別するのは簡単です。

45°、135°、225°のように、45°が絡んだ角度については、\(\displaystyle\frac{1}{\sqrt2}\) 一択
0～1の数直線で、\(\displaystyle\frac12\) はど真ん中
0～1の数直線で、、\(\displaystyle\frac{\sqrt3}{2}\) は1に近い端の方

\(\tan\) の場合

0と値がない場合を除くと、出てくる数字は、\(\sqrt3,~1,~\displaystyle\frac{1}{\sqrt3}\) の3つだけです。区別の方法は、

45°、135°、225°のように、45°が絡んだ角度については、1 一択
\(\sqrt3\) は、1より大きい
\(\displaystyle\frac{1}{\sqrt3}\) は、1より小さい

頭の中で単位円を思い浮かべて一瞬で値を求める

\(120°\)の場合

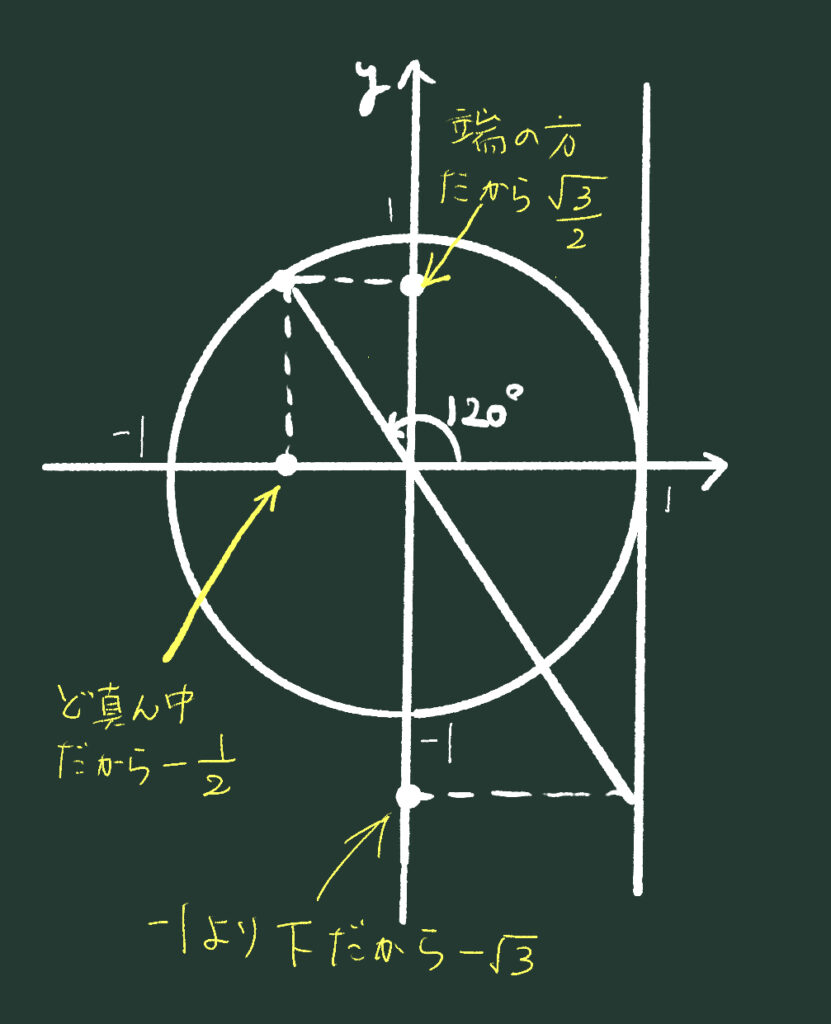
上のような図を、最初のうちは紙の上に書いてもいいですが、慣れてきたら脳内でイメージしましょうう。

\(\sin120°=\displaystyle\frac{\sqrt3}{2},~\cos120°=-\frac12,~\tan120°=-\sqrt3\) ですね。

225°の場合

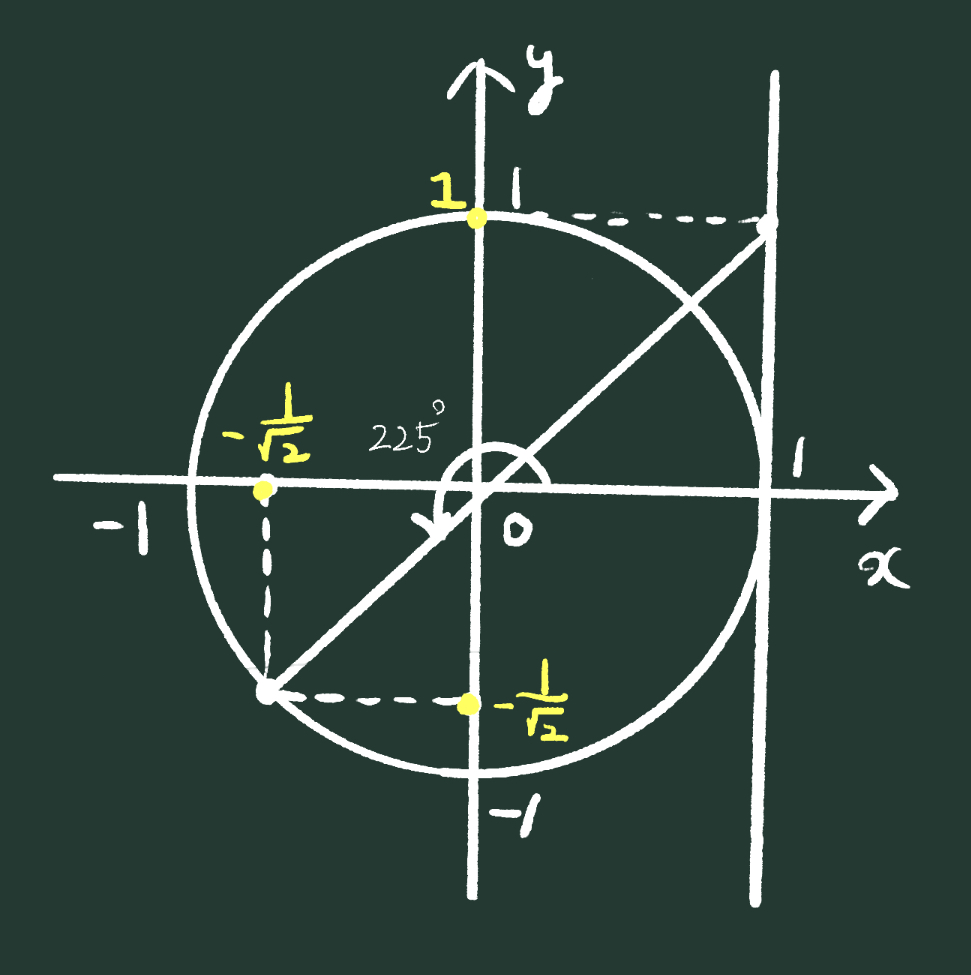
45°が絡んでいると、\(\sin,~\cos\) の座標が微妙な感じですが、\(\displaystyle\frac{1}{\sqrt2}\) 一択なので、後は符号を考えるだけです。

\(\sin225°=-\displaystyle\frac{1}{\sqrt2},~\cos120°=-\frac{1}{\sqrt2},~\tan120°=1\) ですね

PUCFlashでひたすら練習！

やり方が分かったら、後はPUCFlash でひたすら練習します。
最初は、「出題順」で小さい角から順番に、慣れてきたら「ランダム」で練習しましょう。
図を紙に書かず、頭の中でイメージしましょう！
かなり脳を使うので、疲れます。毎日コツコツと練習を積むと、誰でも、52問を3分以内でできるようになります！！