いい問題は探究心を育む

いい問題とは

最近では、TwitterなどのSNSのおかげで、数学の問題に触れる機会が増えてきています。それらを見ていると、つい考えたくなるような問題とそうでない問題があるように思います。いい問題とは、次のように定義されるのではないでしょうか。

問題の意味はわかりやすい。しかし、答を求めることは容易ではない。

逆に、問題の意味はわかりにくいが実際に解いてみると案外あっさりと解けてしまう問題もあります。このような問題は、決していい問題とはいえません。答が求まるかわからないけど、ちょっと解いてみようかなと思わせてくれる問題がいい問題といえます。

いい問題の例

私の趣味は虫食い算を作ることです。虫食い算は、足し算と掛け算さえ理解していれば誰でも挑戦することができます。実際、年賀状に自作の虫食い算の問題を載せると、正月から頭の体操ができたと遠い親戚の方に喜ばれました。

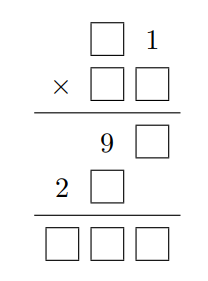
\(58 \times 63\)のような単なる掛け算の問題であれば、計算して答を求めようという意欲は沸き起こりません。しかし、このように少し問い方を工夫するだけで、同じ掛け算の問題あっても印象がまるで異なります。次の問題は、足し算だけできれば理論上解くことができます。

和が2023となるような連続する自然数は何通りあるか求めなさい。

すぐに求まる連続する自然数もありますが、そのすべてを求めることは容易ではないでしょう。自明なもの以外に答はあるのだろうか、あるとしたらどのような自然数なのか、想像するだけで何だか胸がワクワクしてきますね。

「解ける」⇔「面白い」？

数学の面白さを感じるための一つの方法は、問題を解けるようになることです。問題を解けるようになるには、どのように問題にアプローチしていくか（構想力）、答の数値を導出できるか（計算力）などが必要となります。自分の力で答を導き出したときの感動は、何物にも代えがたいものでしょう。

しかし、数学の面白さを感じる方法として、問題を解けるようになること以外に方法はないのでしょうか。そこで、「解ける」と「面白い」の2軸でこの関係をみることにします。

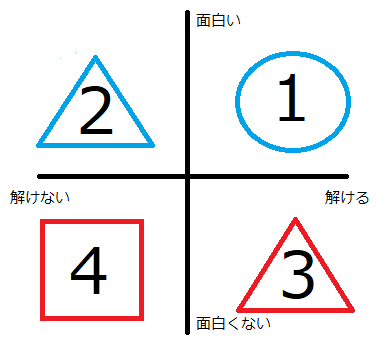
〇１は「解けるから面白い」、□４は「解けないから面白くない」です。どちらも多くの人が経験していることです。△３は「解けても面白くない」です。例えば、足し算を習い始めた小学1年生が\(2 + 3\)の問題を解けたならば、そこから得られる自信によって算数の面白さを感じるかもれません。しかし、大人はこの問題に魅力を感じないでしょう。答を求めることはできますが、それ以上深く考えることはありません。△２は「解けないけれども面白い」です。例えば、

すべての２よりも大きな偶数は2つの素数の和として表せるか

という問題です。この問題はゴールドバッハの予想とよばれており、未解決問題の一つです。\( 4 = 2 + 2, 8 = 3 + 5, 20 = 3 + 17\)など、この予想がある数に対しては成り立つことはわかりますが、これを証明することは容易ではないでしょう。もちろん私も解くどころか解決の糸口さえ見いだせませんが、この問題には数学への憧れといった感情が湧いてきます。

数学が好きになる一つの方法

数学を学ぶ理由は何でしょうか。多くの生徒は、受験で合格点をとるためと答えるでしょう。そのためには、「覚えること」と「練習すること」が必要です。数学の力をつけるためには、この2つは必要です。しかし、数学をさらに深く理解したいのであれば、1つの問題にじっくりと取り組むことが必要です。問題によっては、すぐに解法が思いつかない場合があります。その時に大切なことは、

しっかりと自分の頭で考え続けること

です。その機会を作るためには、やはりいい問題に触れることだと思います。解いてみたいと思える問題は、数学の好奇心を掻き立ててくれます。