答
答は
最も多く現れる最高位の数字は「1」
その個数は25以上33以下
です。ある数に2をかけた数の最高位の数字を調べると、次の通りになります。
| 最高位の数字 | 2をかけた数の最高位の数字 |
| 1 | 2 または 3 |
| 2 | 4 または 5 |
| 3 | 6 または 7 |
| 4 | 8 または 9 |
| 5 | 1 |
| 6 | 1 |
| 7 | 1 |
| 8 | 1 |
| 9 | 1 |
これを図に表すと
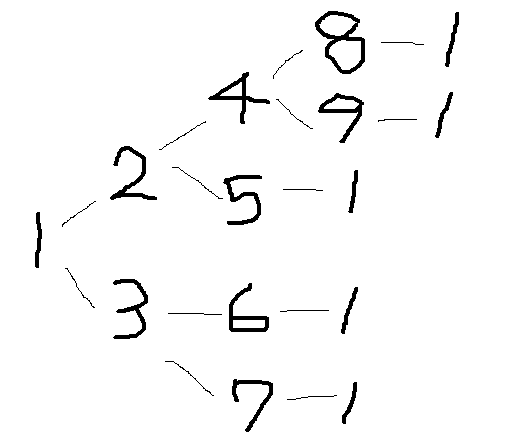
どの数に対しても、2をかけていくと最高位の数字が「1」となる数になります。したがって、もっとも多く出現する数字は「1」となります。
また、周期を調べると
- 短いループは(2,5,1)(3,6,1)(3,7,1)で周期は3
- 長いループは(2,4,8,1)(2,4,9,1)で周期は4
です。したがって、出現割合は\(\displaystyle\frac{1}{4}\)以上\(\displaystyle\frac{1}{3}\)以下となるので、最高位の数字「1」の個数は
25以上33以下
となります。
プログラミングを組んで最高位の数字「1」の個数を求めると、30個でした。コンピューターを用いると個数を正確に求めることができます。
しかし、表のような規則を見つけるだけである程度「1」の個数を推定できるところがおもしろいですね。次のページは生徒の解答です。ここに書いた答より素晴らしいです。



コメント
こんな問題を創作したTommy先生もすごいけど、それに正面から挑む生徒たちもすごいですね。
kを2以上の自然数とする。A(k)={2n|2nはkケタの自然数}とすると、A(k)の要素に最高位の数字が「1」のものがただ一つある。
という発見が、生徒の解答の鍵ですが、これは、実際に書き出して、よく観察する中で、見いだしたものだと思われます。
数学の問題を解くときの、お手本的態度ですね。
いやぁ、お見事でした。
コメントありがとうございます。
生徒たちの意欲というか粘りはすごいです。
こういう姿勢が、国公大学の2次試験で合格点をとるパワーの源になります。